Supervised Fine Tuning on Curated Data is Reinforcement Learning (and can be improved)

Large language models have made big progress over the last years. Today, many of us are already using these models in our daily lives – to give suggestions, to brainstorm ideas, to do research. As we suddenly find ourselves in a situation of societal co-evolution with the models we train, it is more important than ever for us to build a deeper understanding of how society can affect the large machine learning models that we train, and in turn how these models will affect society. As a starting point, we see efforts to simplify our training pipeline to be more amenable for understanding and analysis as a priority.
The large language models of today, are first pre-trained on a large corpus of data. Followed by a specialization phase often referred to as post-training. This post training stage is especially important. Since pre-trained models are, at a high level, generalists. Plainly stated, without any further adaptation or curation, such models may be able to produce answers for many topics but lack specificity. They often produce answers to questions that are, in the best case, relevant to our questions but often vague and in the worst cases hallucinate incorrect statements, potentially misguiding us in our search for answers.
Adoption of large models is, at large, driven by their usefulness for the tasks we might require help with. Predictably, if you ask a hundred people for a specific problem they require help with at any given moment, you will receive a hundred different answers; spanning topics ranging from cooking recipes over help with homework or a deep literature review. We want helpful assistants for many different reasons and many different things. To obtain such models, we need to understand the post-training of a large machine learning model.
Post-training, unlike pre-training, can involve complicated stages of training. It involves stages of further training on curated datasets, a technique known as supervised fine-tuning (SFT) or some form of reinforcement learning (RL). The post-training stage is where we can elicit more elaborate behaviors like reasoning in our models. To achieve this, RL has often been found to be a key ingredient. However, RL has unique set of problems. Firstly, any RL algorithm comes with many "nuts and bolts" that need to be set correctly and make it very difficult to analyze and understand. Secondly, models trained with RL often exploit the reward signals designed to train them, whereby they can hide misalignment. Overall, RL can be difficult to tune and can easily lead to what one may call “user errors” during training – inadvertently training models that are less well aligned than one might hope.
We were motivated by two questions in the start of this project:
- Is there a way we can re-frame the post-training of these large models in a simpler framework that is more amenable to interpretability?
- Can we avoid explicit usage of RL to achieve similar results?
What Our Research Adds To The Picture
Fortunately, for those of us who worry about issues introduced in post-training, recent work has shown that supervised fine-tuning (SFT) alone can be a powerful technique when training is performed on human curated (high quality) datasets. For example, recent work on test time scaling of LLMs (s1) considered fine-tuning a LLM on a small curated reasoning dataset, recovering much of the performance achieved by e.g. OpenAI-o1 and DeepSeek-r1 which relied heavily on RL.
This is good news in two regards: firstly, it shows that post-training can potentially be simplified and, secondly, the process of training on curated data that we can easily inspect is more human interpretable; since it simply boils down to optimizing the dataset to train on.
Loosely connected to these results, the practice of behavioral cloning (e.g. supervised imitation learning) on filtered demonstration data is also the predominant paradigm for training models in many continuous control domains (such as robotics). These results raise an interesting question that we aim to answer in our research: if SFT on curated data can partially close the gap to RL are the two somehow connected? And if they are, can we improve SFT by using this connection?
Our research shows that SFT and RL are indeed connected and we hope that by shining some light on this connection the community will develop better (and easier to interpret) algorithms for post-training in the future.
RL and SFT, two sides of the same coin
To give a bit more detail regarding our work the rest of this blog post contains a sneak peak of the derivation and results. In mathematical terms, our work shows that SFT can be interpreted simply as optimizing a lower bound to the RL objective that we are trying to maximize.
Below we show that the SFT objective bounds the RL objective. Before we do so let's set some notation. Let \(s \in \mathcal{S}\) and \(a \in \mathcal{A} \) denote states and actions in a Markv Decision Process or MDP (for LLMs actions and states are both the same, text tokens). We define a trajectory (e.g. a trace of generated text in an LLM) to be the following \(\tau = (s_0, a_0, \cdots, s_T) \). The actions are drawn from a parametric policy defined by \( \pi(a_t|s_t; \theta)\), we also simplify the notation for the reward from \(r(s_t, a_t)\) to \(r(t)\). The probability of a trajectory is givene by \(p(\tau; \theta) = p(s_0) \prod_{t=0}^{T-1} p(s_{t+1}|s_t, a_t) \pi(a_t|s_t; \theta)\).
SFT Lower Bounds RL
The objective of reinforcement learning is to maximize the reward of generated trajectory (e.g. generated text for LLMs): \[R(\tau) = \sum_{t=0}^T \gamma(t) r(t).\] Here it's is important to note that in a sparse reward setting the reward is only seen at the end of a trajectory and thus can be thought of as a binary signal where \(R(\tau) = 1 \) or \(0\). With these definitions we can write the RL objective as the following \[ \max_{\theta} J(\theta) = \mathbb{E}_{p(\tau; \theta)} [R(\tau)].\] In our paper, we demonstrate that by using the inequality \( x \geq 1 + \log(x)\); we can derive a lower bound on the RL objective as follows: \[ J(\theta) \geq \mathbb{E}_{\pi_{\mathrm{ref}}}\left[R(\tau) \log p(\tau; \theta) \right].\] Now, if we are working in the regime of sparse rewards (such as large language models), this collapses to:\[ J(\theta) \geq \mathbb{E}_{\tau \in \mathcal{D}+}\left[\log p(\tau; \theta) \right].\] Here, \(\mathcal{D}+\) corresponds to a dataset that we have filtered to only contain examples with positive (cumulative) reward. If we are optimizing this right hand side we simply have to maximize the likelihood of data from a curated dataset. If we initialize our model parameters \(\theta\) to the parameters obtained from pre-training then this objective is exactly equivalent to supervised fine-tuning (SFT). Given that the left hand side of the equation above is our RL objective we have thus found a straight-forward relation between RL and SFT.
However, as we also show in our paper, the bound presented above can become extremely loose during training. In this regime, the behavior brought about by supervised fine tuning and RL is still inherently different. A fact best understood by looking at a simple toy example.
Toy Example For Intuition

This toy example is very simple. By which I mean it is actually a bit trivial to think about. So mostly, we are going to illustrate the example with words.
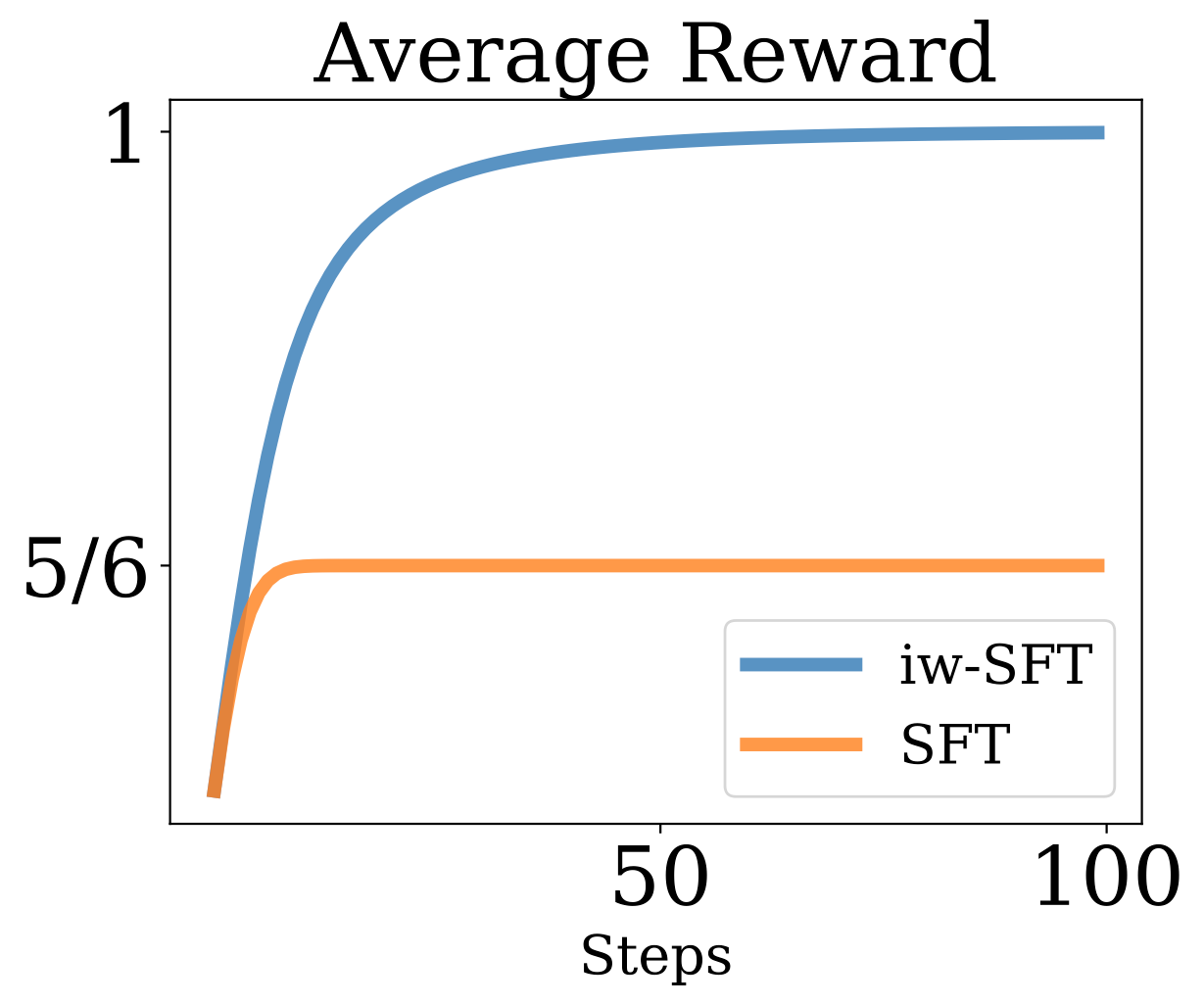
Let's imagine you want to play in a casino. There are two slot machines, each of which has a lever. You can either pull the lever on the right slot machine or you can pull the lever of the left machine. When you pull the machine on the right you are guaranteed to get a dollar as your reward. But when you pull the lever on the machine on the left you get a dollar only with a chance of 50%. In this very simple problem, we can see that the optimal solution is simply to use only the machine on the right.
Of course, when you know the mechanics of the slot machines the solution is obvious. Now suppose, you came here with no knowledge of what each machine does. Instead you are only given a sheet of the record of whenever either of the slot machines has given a pay-out. You see that in two third of the cases on your sheet when a dollar was obtained the machine on the right as used and one third of the time the machine on the left was used. You decide to simply replicate the statistics you find on your sheet; you also try to pull the slot machine on the right two third of the time.
What I have described above is simply SFT. You obtained data of successful attempts and matched it's distribution. As you can see, even in this simple problem, SFT fails to reach the optimal policy. So what can we do to avoid this failure mode? The answer lies in how we can reduce the gap of the bound between SFT and RL. As we show below we can create a better strategy by not only considering the statistics of the successful attempts but by accounting for the strategy that generated these attempts in the first place. For our simple toy example: if you additionally had known that the data on the sheet was produced by a person using either of the machines at random (e.g. pulling either arm with 50% probability) then you could have realized that even though the machine on the left was used 50% of the time it only accounted for one third of the pay-outs and thus must be worse than the machine on the right. This simple re-weighting of observations based on information about the data generating distribution is what we call iw-SFT below (and include in the plot above contrasting the two strategies for the simple slot machine example above).
What can we do to bridge the gap?
So from this we can clearly see that there is much to be improved to bring the bound between SFT and RL closer. And we have already hinted at how we can improve it. In order to solidify this intuition, let us have a look at the derivation of a tighter bound on the RL objective which brings about an algorithm we named: Importance Weighted Supervised Fine Tuning (iw-SFT).
Bringing About a Tighter Bound - iw-SFT
In our paper we show that we can bring about a much tighter bound on the RL objective by introducing an auxiliary probability distribution \(q(\tau)\). Our bound can be written as \[J(\theta)\geq \mathbb{E}_{\tau \in \mathcal{D}+}\left[\frac{q(\tau)}{\pi_{\mathrm{ref}}(\tau)}\log p(\tau; \theta) \right] = \mathcal{I}_{\mathrm{iw-SFT}}\] which, as before, contains the log-likelihood of the curated data but weights it with the ratio of \(q(\tau)\) wrt. the data generating distribution \(\pi_{\mathrm{ref}}(\tau)\). This ratio is what turns SFT into an importance weighted version (iw-SFT). We can see that with the introduction of \(q(\tau)\) we can have control of the tightness of the bound wrt to RL (for derivation please refer to our paper). We also note that the tightness of this bound needs to be traded-off with the distance with respect to the reference policy. On the one hand, when \(q(\tau) \rightarrow p(\tau; \theta) \) the bound tightens. On the other hand, when \(q(\tau) \rightarrow \pi_{\mathrm{ref}}(\tau)\) the variance of the importance weight reduces. Thus this trade-off can now be optimized and chosen.
Understanding the Results
Finally let's have a look at some results. We show that using this new understanding in two different settings, we can obtain improved results. In the first, and most important, setting we consider post-training of a large language model as described above. In particular we follow the setup from the recent paper on simple test time scaling [Muennighoff; 2025] which already considers post-training of LLMs to elicit mathematical reasoning abilities. We check if by tightening the bound (and thus closing the gap to RL) we can obtain better reasoning models for difficult math challenges without abandoning the idea of training only on a human curated dataset. As we can see in the table below this is indeed possible. When starting from the same pre-trained model iw-SFT obtains better results on the benchmarks and does not require extra tricks such as explicitly asking the model to think for longer (which can improve performance of the S1 model from Muennighoff; 2025).
Results for Reasoning
| Model | AIME 2024 | MATH 500 | GPQA Diamond |
|---|---|---|---|
| S1 w/o BF | 50.0 | 92.6 | 56.6 |
| iw-SFT | 66.7 | 94.8 | 64.1 |
Next, to test whether the connection is useful more generally, we considered optimizing smaller policy models for continuous control domains in the well known D4RL benchmark. Here we compare SFT and our importance weighted variant to prominent offline RL algorithms from the literature (full results are in the paper). If we pick out the comparison to Behavior Cloning (BC) (which is just training a policy from scratch on all of the data; thus equivalent to pre-training in this case) and BC on only the top 10% of the data we can again see that our iw-SFT gives consistently better results (and narrows the gap to offline RL methods as shown in our paper).
Results for Control Suite (Medium Replay V2)
| Dataset | BC | BC (10%) | SFT | SFT (Q) | iw-SFT(Q) |
|---|---|---|---|---|---|
| Halfcheetah | 36.6 | 40.6 | 35.1 | 39.3 | 40.9 |
| Hopper | 18.1 | 75.9 | 79.0 | 84.9 | 85.0 |
| Walker2d | 26.0 | 62.5 | 58.8 | 66.2 | 75.8 |
Learning More
If you find this perspective intriguing you can read more in our detailed report published on arXiv.
Additionally, if you want to build on the ideas we presented above, in the spirit of spreading understanding we made all our code and models freely available for anyone to use. You can find code, at GitHub, for language here and for control here. The reasoning model trained with our approach can be found on Hugging Face.
If you have questions, want to get involved in some form, or want to help us along, you can reach at contact@independentresearch.ai.